
CONGRUENCIA Y SEMEJANZA DE TRIANGULOS
Semejanza:
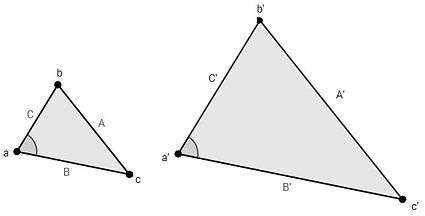
Dos triángulos son semejantes si sus ángulos son respectivamente congruentes (iguales) y sus lados proporcionales. Es decir, tienen la misma forma sin importar los tamaños entre ellos. Se simboliza:


Criterios de semejanza:
-
Angulo - Angulo (AA): Dos triángulos son semejantes si tienen dos ángulos respectivamente congruentes.

-
Lado - Ángulo - Lado (LAL): Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos congruentes.

-
Criterio Lado - Lado - Ángulo (LLA): Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo opuesto al mayor de ellos son congruentes.


Ejemplo:
Los siguientes triangulos son semejantes, hallar la medida de los lados C y A'

Si los triángulos son semejantes, por definición:
A = B = C = r (razón de proporción)
A' B' C'
Por lo tanto, si reemplazamos los valores de B y B' hallaremos r:
B = 6 = 0,6
B' 10
Entonces:
A = 12 = 0,6 Despejamos A'
A' A'
12 = 0,6 . A'
12 : 0,6 = A'
20 = A'
Repetimos el procedimiento para hallar C:
C = C = 0,6 Despejamos C
C' 7,5
C = 0,6 . 7,5
C = 4,5cm
Actividades:
1) Plantear la proporcionalidad de los tres lados sabiendo que los triángulos son semejantes.

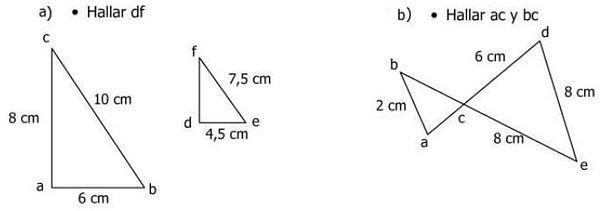
2) Hallar el valor del lado que se pide en cada caso, sabiendo que los triángulos son semejantes.
3) Demostrar que los triángulos son semejantes.

4) Para demostrar que Δ ABD ~ Δ EDC, ¿Qué criterio de semejanza usarías? Justifica.










