
CONJUNTO DE NUMEROS COMPLEJOS
Numeros Imaginarios
Para dar solución a una raíz par con radicando negativo es necesario definir lo que es un numero imaginario, ya que trabajando con el conjunto de los números reales no podremos encontrar dicha solución. Entenderemos mejor guiándonos con un ejemplo:

Como vimos en la sección de radicales, √-9 no tiene solución en el conjunto de los números reales, es decir, no existe ningún número real tal q dicho numero al cuadrado nos de -9
Si reescribimos el radical de la siguiente forma y aplicamos propiedad distributiva obtendremos..
√9 que tiene solución real, 3 y √-1 que la definiremos como i
La unidad imaginaria es el número √-1 y se designa por la letra i
Por lo tanto un numero imaginario esta compuesto por un numero real seguido de la unidad imaginaria
Propiedades

Se repite el patrón de cuatro en cuatro por eso, para saber cuánto vale una determinada potencia de i, se divide el exponente entre 4, y el resto es el exponente de la potencia equivalente a la dada. Ejemplo:

Numeros Complejos
Un numero complejo en su forma binomica se expresa como a + bi donde "a" es la parte real y "bi" un imaginario
Un real puro puede escribirse como "a+oi"; de igual forma, un imaginario puropuede escribirse como "o+bi" por lo tanto el conjunto de los numeros reales y el conjunto de los numero imaginarios estan contenidos en el conjunto de los numeros Complejos.

Un numero complejo tambien puede expresarse como un par ordenado (x,y) donde x es la parte real e y la parte imaginaria
Podemos representar todo numero complejo como un vector que va desde el origen hasta el punto (x,y)

Ejercicio:

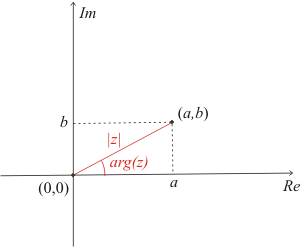
Módulo y argumento de un número complejo
Sea z un número complejo cualquiera. Llamaremos módulo del número complejo , al número real dado por |z| =
(Ver Teorema de Pitágoras). El módulo se interpreta como la distancia al origen del número (Gráfica 2).
Por otra parte, llamaremos argumento del número complejo z, al ángulo comprendido entre el real y el vector. El argumento de se denota como arg(z) y se calcula mediante la expresión:
Nota: Ver Razones trigonométricas.
Forma trigonométrica o polar de un número complejo
La forma trigonométrica de un número complejo se establece a partir del triángulo rectangulo que se forma con el vector que representa el numero complejo como hupotenusa, el segmento vertical "y" es el cateto opuesto y el segmento horizontal "x" el cateto adyacente.
A partir de las razones trigonometricas podemos establecer que:
x = r.cos θ
y = r.sen θ
Para todo complejo en su forma binomica z = x + yi reemplazamos x e y:
z = r.cos θ + r.sen θ i
z = r (cos θ + i.sen θ)

Ejemplo: Dado z = 1-i, lo escribiremos en su forma trigonométrica.
1) Primero determinamos el modulo de z, es decir, |z|

2) Determinamos el arg(z) = θ

Por lo tanto, el numero complejo z será expresado en su forma trigonométrica como:

Para llevar un número de su forma trigonométrica a la biónica simplemente calculamos el seno y coseno del Angulo, y aplicamos propiedad distributiva del modulo.
Ejemplo:

Forma Polar:
Expresar un número complejo en su forma polar es simplemente escribir su modulo "r" seguido del ángulo "θ" como subíndice:
Ejemplo:

Forma exponencial:
Un número complejo en su forma exponencial se expresa de la siguiente forma:
Ejemplo:

Ejercicio
Escribe en forma trigonométrica, polar, y exponencial los siguientes números complejos:
a) 4 + 3i b) -1 + i c) 5 - 12i
Escribe los siguientes números en su forma biónica
a) 3(cos 60° + i sen 60°)
b) 3(cos 135° + i sen 135°)
c) cos 270° + i sen 270°
Opuesto de un numero complejo:
Sea z = x + yi entonces su opuesto sera -z = -x -yi
Conjugado de un numero complejo:
Sea z = x + yi entonces su conjugado sera z' = x - yi
Observación: Note que el opuesto de un complejo esta formado por el opuesto de ambas partes, real e imaginaria a diferencia del conjugado, en este ultimo solo cambia el signo de la parte imaginaria

Ejercicios.

Suma y Resta
Para sumar números complejos simplemente seguimos las reglas básicas de la matemática agrupando los números reales y los números imaginarios respectivamente.
(a+bi)+(c+di)=(a+c)+(b+d)i
Ejemplo:
(5+3i)+(2+6i) = (5+2)+(3i+6i) = 7+9i
Para realizar una resta, también se deben agrupar los números reales e imaginarios pero debemos tener mas cuidado con los signos, por eso recomiendo que antes de agrupar debemos aplicar la propiedad distributiva del signo negativo.
Ejemplo:
(5 - 2i) - (2 + 6i) =
5 - 2i - 2 - 6i =
(5 - 2) + (-2 - 6)i=
3 + (-8)i=
3 - 8i
Multiplicación
Para la multiplicación debemos aplicar propiedad distributiva.
(a + bi).(c + di) =
a.c + a.di + bi.c + bi.di =
ac + adi + bci + bdi²=
ac + adi + bci - bd =
(ac - bd) + (ad + bc)i =
Nota: Podemos observar que el elemento bdi² se convierte en –bd por la propiedad de los números imaginarios en la cual i² es igual a -1.
Ejemplo:
(3+2i)(6+7i) =
3.6 + 3.7i + 2i.6 + 2i.7i=
18 + 21i + 12i + 14i²=
18 + 21i + 12i -14=
(18 - 14) + (21 + 12)i =
4+33i
División
Para dividir dos números complejos debemos operar igual que con la racionalización. Y de igual manera tendremos dos posibles casos:
1er Caso) El divisor es un imaginario puro
Ejemplo:

Como se puede observar, el divisor es un numero imaginario puro
Aplicamos propiedad uniforme: Multiplicamos a nuestra expresion por una fraccion con igual numerador y denominador
Resolvemos el producto de fraccion aplicando propiedad distributiva en el numerador
Reemplazamos i²por -1 (propiedad de potencia de los numeros imaginarios)
Ya solo nos queda separar en dos terminos la parte real de la parte imaginaria:
Distribuimos el denominador en ambos terminos del numerador
Simplificamos de ser posible
Eliminamos el parentesis aplicando regla de signos
2do Caso) El divisor es un complejo con parte real e imaginaria.
Ejemplo:

Como podemos observar, el denominador es un numero complejo compuesto por una parte real y una parte imaginaria.
Aplicamos propiedad uniforme: En este caso siempre el numerador y denominador de nuestra nueva fraccion sera el conjugado del denominador de nuestro ejercicio. En este caso el denominador es 2-3i asique nuestra fraccion tendra como numerador y denominador 2+3i
Multimplicamos realizando propiedad distributiva. Si lo hacemos correctamente siempre nuesto segundo y tercer termino seran opuestos, por lo que podremos cancelarlo y nuestro ultimo termino tendra un i²
Reemplazamos i² por -1 (propiedad de potencia de los numeros imaginarios)
Ya solo nos queda separar en dos terminos la parte real de la parte imaginaria:
Distribuimos el denominador en ambos terminos del numerador
Simplificamos de ser posible (en este ejemplo no podemos)
Ejercicios.
