
FUNCION
Definición de Relación
Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado Imagen o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos de la Imagen o Rango.
Ejemplo: El siguiente diagrama sagital muestra la relacion A es hermano de B

Como resultado de corresponder elementos del dominio con elementos del rango es pues, una relacion. Entonces:
Una relacion R es un conjunto formado por pares ordenados (a,b) siendo "a" elementos del dominio y "b" elementos del rango.
Definiremos los conjuntos de la grafica de forma analitica:
Dados los conjuntos A = {Ariel, German, Jorge} y B = {Mariana, Ines, Carina, Cecilia}
Definimos R por comprension: R = {Todo par ordenado (a,b) tal que a pertenece a A, b pertenece a B y a es hermano de b}
Definimos R por extension: R = {(Ariel,Marina) ; (German,Ines) ; (Jorge,Carina) ; (Jorge,Cecilia)}
Ejemplo 2:
Definimos la relacion: a R b sii a < b con a, b = Numeros de un dado
Entonces: A = {1,2,3,4,5,6}
B = {1,2,3,4,5,6}
Definimos la relacion por extension:
R = {(1,2) ; (1,3) ; (1,4) ; (1,5) ; (1,6) ; (2,3) ; (2,4) ; (2,5) ; (2,6) ; (3,4) ; (3,5) ; (3,6) ; (4,5) ; (4,6) ; (5,6)}

Observacion:
Nota que, dado el ejemplo anterior, no existe el par ordenado (3,2) puesto que 3 no es menor que 2, por esta razon es muy importante recalcar que los elementos de la relacion son elementos ordenados, no es lo mismo decir (2,3) que (3,2)
Esta y cualquier relacion puede ser graficada en un sistema de ejes cartesianos.
-
Sistema de ejes cartesianos:
Un sistema de ejes cartesianos lo forman dos rectas perpendiculares entre sí, El eje horizontal se llama eje de abscisas y representa los valores del dominio (x) . El eje vertical se llama eje de ordenadas y representa los valores del conjunto rango (y).
Las coordenadas de un punto cualquiera P se representan por el par ordenado (x, y).
El punto o donde se cortan los dos ejes se llama origen de coordenadas y sus coordenadas son (0,0)
Los ejes de coordenadas dividen al plano en cuatro partes iguales y a cada una de ellas se les llama cuadrante.

Para graficar la relacion de nuestro ejemplo de los dados debemos graficar un punto por cada par ordenado de nuestro conjunto R asi pues, para ubicar el punto de coordenada (1,2) debemos desplazarnos desde el origen, una unidad hacia la derecha por el eje de las absisas y subir dos unidades paralelo al eje de las ordenadas. Para ubicar el (4,5) nos desplazamos 4 a la derecha y 5 hacia arriba.
Como los valores de los dados son todos positivos, todos los puntos estaran ubicados en el 2do cuadrante

Ejercicios
1) Representa los siguientes pares ordenados en un sistema de ejes cartesianos: A=(1, 3), B=(-2, 5), C=(-3, -4), D=(5, -3), E=(0,4) y F=(4,0)
2) Determina las coordenadas de los siguientes puntos

3) Determina el dominio y rango de las siguientes relaciones
R = { (– 3, – 6), (– 2, – 4 ), (– 1, – 2), ( 0, 0 ), ( 1, 2 ), ( 2, 4 ) }
R = { (– 2, –1), (– 1, 0 ), ( 0, 1 ), ( 1, 2 ), ( 2, 3 ) }
R = { ( 4, 2), ( 4, – 2 ), ( 9, 3 ), ( 9, –3 )}

Definicion de Funcion
Una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Rango.
Ejemplo: En una tienda comercial, cada artículo está relacionado con su precio; o sea, a cada artículo le corresponde un precio.
Por lo tanto podemos afirmar que toda funcion es una relacion, pero no toda relacion es una funcion.
Ejercicio:
Determina cual de las siguientes relaciones son funciones.

Graficamente podemos determinar si una relacion es funcion o no usando el criterio de la recta vertical, este criterio consiste en trazar rectas verticales en la de modo que intersecte la grafica, en una funcion las rectas intersectan a la grafica en un solo punto, de no ser asi, la relacion no es funcion.
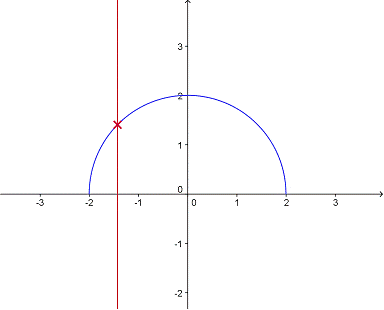
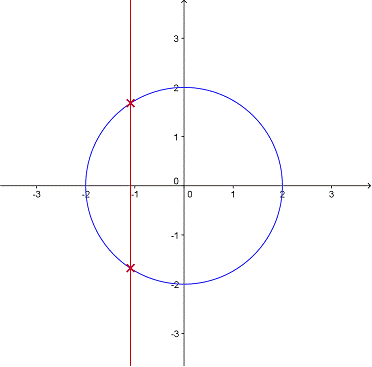
Como se ve en la grafica de la izquierda la recta vertical intersecta una unica vez a la grafica y toda recta que se dibuje sera de igual manera. En cambio, en la grafica de la derecha, la recta vertical intersecta a la grafica mas de una vez, en dos puntos, por lo tanto esta no es una funcion.
Nota: Basta con que una sola recta intersecte a la grafica en mas de un punto para determinar que la relacion no es funcion.
Ejercicio
Determina cual de las siguientes relaciones son funciones

